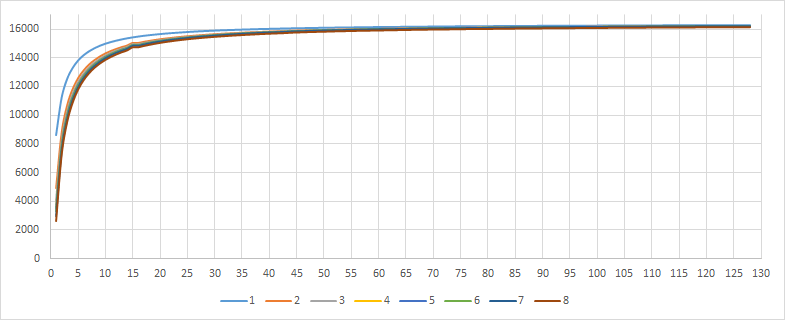Introduction
At the current moment, EscapeFreq for a specific context equals the number of symbols in that context. This leads to the problem of assigning ESC codes that are either too short or too long in same cases. To make the estimation for the ESC symbol more precise, we need in some way to collect statistic about successful and unsuccessful symbol encoding cases dynamically. If we use PPM, we expect a clear correlation between Order-N contexts, so we will collect statistic about encoding success not for each context separately, but for the entire model as a whole. This way, similar contexts that may not occur frequently individually but occur regularly in the overall will receive a more accurate estimation. Thus, we have our main model, that collect statistics about our data, and a secondary model that adjust it based on the data obtained by observation on contexts.
Such a method of estimation the ESC symbol probability called SEE (Secondary Escape Estimation). One of the first who proposed a working version of this idea was Charles Bloom in his work on PPMZ [1][2] back in 1996, as far as I understand. If you’re interested in the topic of PPM, you definitely need to take a look at a more advanced implementation of it. We will explore another method of implementing SEE called PPMII, proposed by Dmitry Shkarin in 2001[3]. You might have seen implementation of this method under the name PPMd.
PPMII can be considered as one of the last significant advancements in PPM (I might be mistaken, but that’s the impression I have, as it is mentioned most frequently on the Internet), that’s why I decided to stop on it. The author of PPMII is an absolutely non-public person, so I can’t provide any information about him. I was only able to find examples of implementation on this website; any mentions of PPMII seem to refer back to this site. There are various versions of the implementation by the author that you can explore. During the writing of this article, I came across an implementation of the J version (sort of latest)[4] by person who happens to be the administrator of what is presumably the main forum dedicated to compression encode.su (and if believe from what I found he also countryman of mine, that just was cool for me to find out). So you can check this implementation of J version, maybe you will find it more readable or if you don’t trust the website that I’ve referred to first.
The difference between the PPMd method lies in how the contexts are quantized and how the data is adapted within them. The author made these choices based on his statistical research, and as far as I understand, it was targeted for PPM-style data (e.g., text), but data that doesn’t fit perfectly was also taken into account. This means that in theory, you can optimize modeling of SEE for a specific type of data, taking PPMd as an example. This sounds cool, but I doubt that it is useful in practice. That’s why all constant numbers that you will see should be perceived as an example and not the truth of how SEE should be done. The method of context building from the previous part was obviously not invented by myself; I just accidentally discovered it when I was looking at the PPMd implementation as a bonus. I didn’t mention this earlier to not disturb the reader on the SEE subject. Here we will look at the F version, explore new techniques, and I will try to provide some comments. In the end, I hope you will understand the idea of SEE.
SEE data
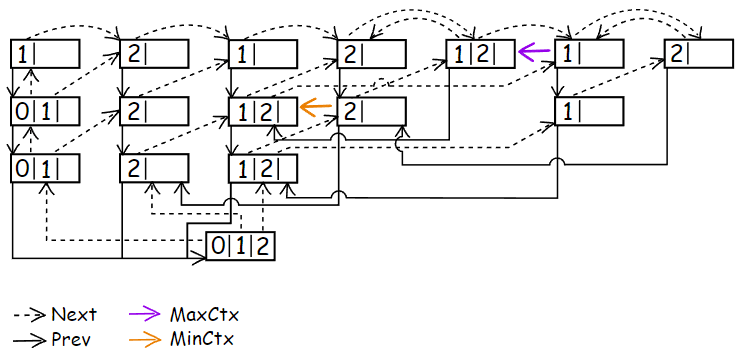
Let’s look at the image from the previous part with randomly placed MinContext on it.
A complete list of parameters by which we can divide contexts based on the significance of their influence you can check in the author’s work (although it may not exactly match the latest versions of PPMd). I’ll list only the parameters that we will use:
- the frequency of the symbol in the binary context
- the count of the symbol in the context
- the difference in symbol count between current CM(k) and its child CM(k - 1)
- the count of the previous masked symbols from CM(k + 1)
- the difference between the count of masked symbols and the count of symbols in the current context
- the ratio of the total frequency of all symbols in the current context to the count of symbols in it.
We can also consider the order of the context, but the PPMII style of SEE doesn’t use it, unlike PPMZ. To obtain useful information from the gathered statistics, we don’t use every possible combination of values from the enumerated parameters but rather quantize them to a reasonable range. The more a parameter affects the accuracy of prediction of exiting from a context event, the more useful it will be to have more values for it after quantization.
We will introduce several new functions for encoding and decoding, but this time I will not show code for decoding to save time and space and because it is 90% the same as the encoding code. So if you have already read the previous two articles on PPM, you will easily understand the decoding part without my comments.
We start by adding a pointer to the SEE class and allocating memory for it separately in the constructor.
1
2
3
4
5
6
7
8
9
10
11
12
13
class PPMByte
{
SEEState* SEE;
...
PPMByte(u32 MaxOrderContext, u32 MemLimit = 0) :
SubAlloc(MemLimit), SEE(nullptr), OrderCount(MaxOrderContext)
{
SEE = new SEEState;
initModel();
}
~PPMByte() { delete SEE; }
}
It was challenging to choose the right order of presenting the material so that it flows smoothly. So, let’s first examine the structure and initialization of the static data for the new SEEState class. The rest will be overgrown with details in the course of this part.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
struct see_context
{
u16 Sum;
u8 Shift;
u8 Count;
};
struct see_bin_context
{
u16 Scale;
};
class SEEState
{
public:
see_context* LastUsed;
u8 PrevSuccess;
u8 NToIndex[256];
u8 DiffToIndex[256];
see_context Context[44][8];
see_bin_context BinContext[128][16];
public:
SEEState()
{
u32 i;
for (i = 0; i < 6; i++) NToIndex[i] = 2 * i;
for (; i < 50; i++) NToIndex[i] = 12;
for (; i < 256; i++) NToIndex[i] = 14;
for (i = 0; i < 4; i++) DiffToIndex[i] = i;
for (; i < (4 + 8); i++) DiffToIndex[i] = 4 + ((i - 4) >> 1);
for (; i < (4 + 8 + 32); i++) DiffToIndex[i] = 4 + 4 + ((i - 4 - 8) >> 2);
for (; i < 256; i++) DiffToIndex[i] = 4 + 4 + 8 + ((i - 4 - 8 - 32) >> 3);
}
}
The NToIndex array represents quantized values of symbol count in the child context, which we will use for searching SEE contexts for binary contexts of the main model. DiffToIndex is the quantized values of the difference between the masked count of symbols and the count of symbols in the current MinContext. If we have just started encoding a symbol in a non-binary context, as shown in image, then at this time we don’t have the masked symbol yet. This will be a separate case for which we will not be doing a search for SEE context.
Each type of binary and non-binary context at the start has some pre-initialized optimized value determined by the author during his research. Thus, at the start of the model and after a reset() call, we need to initialize them.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void initModel()
{
...// init PPM stuff
SEE->init();
}
static constexpr u32 CTX_FREQ_BITS = 7;
static see_context SEEState::initContext(u32 Init)
{
see_context Result;
Result.Shift = CTX_FREQ_BITS - 3;
Result.Sum = Init << Result.Shift;
Result.Count = 16;
return Result;
}
void SEEState::init()
{
PrevSuccess = 0;
LastUsed = &Context[43][0];
static const u16 InitBinEsc[16] = {
0x3CDD, 0x1F3F, 0x59BF, 0x48F3, 0x5FFB, 0x5545, 0x63D1, 0x5D9D,
0x64A1, 0x5ABC, 0x6632, 0x6051, 0x68F6, 0x549B, 0x6BCA, 0x3AB0};
for (u32 i = 0; i < 128; i++)
{
for (u32 j = 0; j < 16; j++)
{
BinContext[i][j].Scale = FREQ_MAX_VALUE - (InitBinEsc[j] / (i + 2));
}
}
for (u32 i = 0; i < 44; i++)
{
for (u32 j = 0; j < 8; j++)
{
Context[i][j] = SEEState::initContext(4 * i + 8);
}
}
}
In addition to the previously listed parameters by which we can group contexts, we also have PrevSuccess which indicates whether the previous symbol was successfully encoded. We will use this information only during encoding from binary contexts, like this:
1
2
3
4
5
6
inline see_bin_context& getBinContext(context* PPMCont)
{
u32 CountIndex = PrevSuccess + NToIndex[PPMCont->Prev->SymbolCount - 1];
see_bin_context& Result = BinContext[PPMCont->Data[0].Freq - 1][CountIndex];
return Result;
}
As you can see now, all 128 values of the BinContext array are directly mapped to the frequency counter of the symbol in binary context. The frequency counter for a symbol in a binary context will increase by 1 instead of by 4, which is why we will not jump over values in the array. If you remember, for regular contexts, we call rescale() if at least one symbol exceeds Freq > 124, but we make an exception for binary context and will not do rescale for them. Each even CountIndex corresponds to a previous unsuccessful encoding attempt, and each odd to a successful one. The InitBinEsc array is used precisely to assign more accurate initial values for each case. The FREQ_MAX_VALUE value was not changed and is still equal to 2^14. The first graphic shows value for even values and the second for odd.
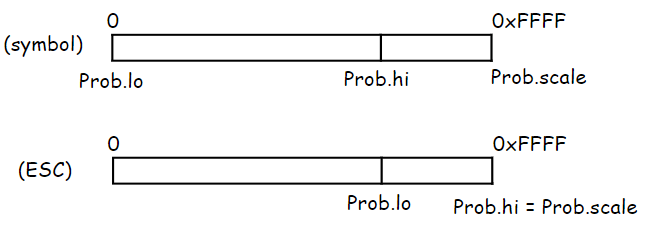
The main difference is focused on the initial values of the symbol occurrence frequency, and then they quickly level off, almost reaching FREQ_MAX_VALUE. The point here is that when encoding a binary context, we specify the probability only for the symbol itself and ESC. We can map the proportion occupied by each by simply shifting the values of Prob.lo and Prob.hi while maintaining the value of Prob.scale the same.
That is, the value of see_bin_context::Scale shows the range that symbol will take for its encoding. Additionally, as consequence of having Prob.scale as 2^14 for encoding only two values, it allows us to set the probability for encoding more precisely. If you remember, in the part about AC, I mentioned that AC only encoding ranges, and their interpretation is our job.
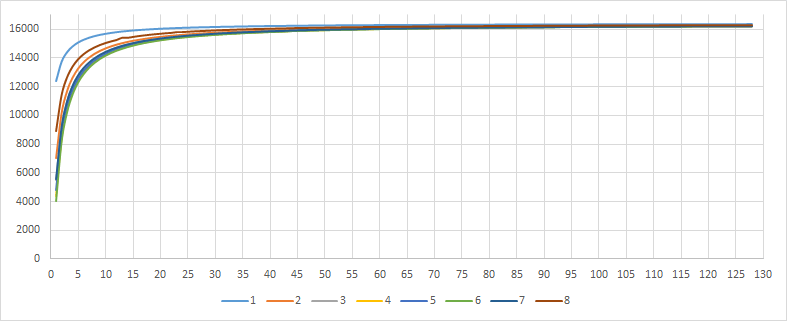
We will use the values of non-binary contexts in a different way, and it will be better understood through examples. So, to avoid confusion, I will simply show you a graph of their start values for now:
Encoding
binary
As I have said at the beginning, we now have three types of contexts from which we do encoding:
- binary
- non-binary without masked symbol
- non-binary with masked symbol.
The first two can only occur at the beginning of the symbol encoding process. So, we add them:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void encode(ArithEncoder& Encoder, u32 Symbol)
{
prob Prob = {};
b32 Success = false;
if (MinContext->SymbolCount == 1)
{
Success = getEncodeProbBin(Prob, Symbol);
}
else
{
Success = getEncodeProbLeaf(Prob, Symbol);
}
Encoder.encode(Prob);
while (!Success)
{
...// try to find encode symbol
}
...// update
}
We can finally see how we use SEE context for encoding in a binary context:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
static constexpr u32 INTERVAL = 1 << CTX_FREQ_BITS;
static const u8 ExpEscape[16] = {25, 14, 9, 7, 5, 5, 4, 4, 4, 3, 3, 3, 2, 2, 2, 2};
b32 PPMByte::getEncodeProbBin(prob& Prob, u32 Symbol)
{
b32 Success = false;
Prob.scale = FREQ_MAX_VALUE;
see_bin_context& BinCtx = SEE->getBinContext(MinContext);
context_data* First = MinContext->Data;
if (First->Symbol == Symbol)
{
LastEncSym = First;
Prob.lo = 0;
Prob.hi = BinCtx.Scale;
First->Freq += (First->Freq < 128) ? 1 : 0;
BinCtx.Scale += INTERVAL - SEE->getBinMean(BinCtx.Scale);
SEE->PrevSuccess = 1;
Success = true;
}
else
{
SEE->PrevSuccess = 0;
Prob.lo = BinCtx.Scale;
Prob.hi = FREQ_MAX_VALUE;
BinCtx.Scale -= SEE->getBinMean(BinCtx.Scale);
InitEsc = ExpEscape[BinCtx.Scale >> 10];
LastMaskedCount = 1;
Exclusion->Data[First->Symbol] = 0;
}
return Success;
}
I just mentioned how the probability for the symbol and ESC is set, and that we increment the counter by 1. However, I didn’t explain what happens next with the SEE context value. We’re begin adapting it!
1
2
3
4
5
6
7
u8 SEEState:getBinMean(u16 Scale)
{
u32 Shift = 7;
u32 Round = 2;
u8 Result = (Scale + (1 << (Shift - Round))) >> Shift;
return Result;
}
We calculate the average value of Scale / TestCount, where TestCount is fixed and is equal to the power of two, so we can replace divide with a bitwise shift. Adding 1 << (Shift - Round), as I understand, is for rounding up value due to carry propagation. For example:
0b101100 >> 4 = 0b10
(0b101100 + 0b100) >> 4 = 0b11
The larger the value of BinCtx.Scale, the smaller the difference INTERVAL – MEAN. Due to rounding up, we can fix the maximum value of BinCtx.Scale because when its value rounds up to FREQ_MAX_VALUE, the added value will be 0. In the case of an unsuccessful encoding attempt, on the contrary, the larger the value of BinCtx.Scale, the faster we expand the range for encoding the ESC symbol. But here’s one more detail. If we encode ESC, it means that after execution of update(), this context will no longer be binary. The smaller value of BinCtx.Scale at this moment, the more likely we will see a new symbol in this context in the future, and vice versa. For this reason, we initialize the value of InitEsc to represent the portion that ESC occupies in the TotalFreq value.
non-binary without masked
If we start from a non-binary context from the beginning, we check the first symbol (later symbol that called rescale() will be moved to first place in the list).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
b32 getEncodeProbLeaf(prob& Prob, u32 Symbol)
{
b32 Result = false;
Prob.scale = MinContext->TotalFreq;
context_data* First = MinContext->Data;
if (First->Symbol == Symbol)
{
LastEncSym = First;
SEE->PrevSuccess = ((First->Freq * 2) > MinContext->TotalFreq) ? 1 : 0;
Prob.lo = 0;
Prob.hi = First->Freq;
MinContext->TotalFreq += 4;
First->Freq += 4;
if (First->Freq > MAX_FREQ)
{
rescale(MinContext);
}
Result = true;
}
else
{
...// try to encode symbol
}
}
If the symbol occurs frequently in the current context and its probability is greater than 50%, we consider that we are in a data block that has a clear pattern, and we set PrevSuccess to 1. In other cases, as before, we start searching for this symbol in the context.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
b32 getEncodeProbLeaf(prob& Prob, u32 Symbol)
{
b32 Result = false;
Prob.scale = MinContext->TotalFreq;
context_data* First = MinContext->Data;
if (First->Symbol == Symbol)
{
...// encode, set SEE->PrevSuccess if symbol prob > 50%
}
else
{
SEE->PrevSuccess = 0;
Prob.lo = First->Freq;
u32 SymbolIndex = 1;
context_data* MatchSymbol = nullptr;
for (; SymbolIndex < MinContext->SymbolCount; ++SymbolIndex)
{
MatchSymbol = MinContext->Data + SymbolIndex;
if (MatchSymbol->Symbol == Symbol) break;
Prob.lo += MatchSymbol->Freq;
}
...// check if found match
}
return Result;
}
But the way, as you could see, we don’t use the Exclusion array now when we don’t need it. The part that is responsible for encoding the symbol in getEncodeProbLeaf() is a little bit different from how we do it in getEncodeProb().
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
b32 getEncodeProbLeaf(prob& Prob, u32 Symbol)
{
b32 Result = false;
Prob.scale = MinContext->TotalFreq;
context_data* First = MinContext->Data;
if (First->Symbol == Symbol)
{
...// encode, set SEE->PrevSuccess if symbol prob > 50%
}
else
{
...// try to find match
if (SymbolIndex < MinContext->SymbolCount)
{
Prob.hi = Prob.lo + MatchSymbol->Freq;
MinContext->TotalFreq += 4;
MatchSymbol->Freq += 4;
context_data* PrevSymbol = MatchSymbol - 1;
if (MatchSymbol->Freq > PrevSymbol->Freq)
{
swapContextData(MatchSymbol, PrevSymbol);
MatchSymbol = PrevSymbol;
}
LastEncSym = MatchSymbol;
if (MatchSymbol->Freq > MAX_FREQ)
{
rescale(MinContext);
}
Result = true;
}
else
{
Prob.hi = Prob.scale;
LastMaskedCount = MinContext->SymbolCount;
updateExclusionData(MinContext);
}
}
return Result;
}
And it differs in that we swap context_data if the symbol that we have successfully encoded has a frequency greater than the previous one. If the required symbol was not found, we add the symbol to the Exclusion array and save the total count of the symbol in this context for the next step. After that, we go down the chain of child context and encode the symbol or ESC in getEncodeProb().
non-binary with masked
In this case, we will again use the value obtained from SEE context, but now it is for non-binary context. Let’s look at how we search and get the value from see_context:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
u16 SEEState::getMean(see_context* Context)
{
u32 Result = Context->Sum >> Context->Shift;
Context->Sum -= Result;
Result = Result ? Result : 1;
return Result;
}
u16 SEEState::getContextMean(context* PPMCont, u32 Diff, u32 MaskedCount)
{
u16 Result;
if (PPMCont->SymbolCount != 256)
{
u32 Index = 0;
Index += (Diff < (PPMCont->Prev->SymbolCount - PPMCont->SymbolCount)) ? 4 : 0;
Index += (PPMCont->TotalFreq < (11 * PPMCont->SymbolCount)) ? 2 : 0;
Index += (MaskedCount > Diff) ? 1 : 0;
LastUsed = &Context[DiffToIndex[Diff - 1]][Index];
Result = getMean(LastUsed);
}
else
{
LastUsed = &Context[43][0];
Result = 1;
}
return Result;
}
Where:
MaskedCount = LastMaskedCount
Diff = SymbolCount – LastMaskedCount
First, we divide a context into two types based on the count of unmasked symbols in the next CM(k-1) that we would have if we fail to encode a symbol in the current MinContext.
Then each group is further divided into two subgroups based on the ratio of (TotalSymbolFreq + EscapeFreq) to the number of symbols in the context. Why should TotalFreq be 11 times greater than SymbolCount? That’s how the author decided. If you think about it, it’s not that much. For example, if we have 10 symbols in the context with ESC it’s ~10 points for each symbol if they had equal frequency value. Initially, I thought that by doing this, the author was trying to separate contexts where the statistics do not reflect a clearl pattern. However, it seems more likely that it is the ratio of average symbol frequency to the number of exits from the context (that indicated by the symbol count) that is being checked. This is also what the author writes about in the section on evaluating the exit probability from such contexts (what I get from another run through the paper). And finally, there is the ratio of the number of masked symbols to the unmasked symbols.
We only add SEE usage to the body of the function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
b32 getEncodeProb(prob& Prob, u32 Symbol)
{
b32 Result = false;
u32 MaskedDiff = MinContext->SymbolCount - LastMaskedCount;
Prob.scale = SEE->getContextMean(MinContext, MaskedDiff, LastMaskedCount);
...// try to find symbol
if (SymbolIndex < MinContext->SymbolCount)
{
...// compute rest of Prob struct
...// Prob.scale = MaskedTotalSymbolFreq + ESC freq from see_context
Result = true;
}
else
{
Prob.scale += Prob.lo;
Prob.hi = Prob.scale;
SEE->LastUsed->Sum += Prob.scale;
LastMaskedCount = MinContext->SymbolCount;
updateExclusionData(MinContext);
}
return Result;
}
For binary context, the value see_bit_context reflects the accumulated statistics for a symbol in the current context, and we use the average value for continuous scaling of this probability.
In the case of non-binary contexts, the average value obtained from see_context is used only to determine the proportion occupied by ESC in the total sum of Prob.scale. This value is decreased by MEAN if the symbol was encoded and increased by MaskedTotalSymbolFreq + MEAN a failed attempt. That is, the smaller the value of Sum in see_context, the smaller the MEAN value will be, the smaller the range ESC will occupy. The Shift value is not static as in the case of see_bin_context. During the update() call, we will update the value of Count for SEE->LastUsed. The way this happens has also changed between different versions.
1
2
3
4
5
6
7
8
void SEEState::updateLastUsed(void)
{
if ((LastUsed->Shift < CTX_FREQ_BITS ) && (--LastUsed->Count == 0))
{
LastUsed->Sum += LastUsed->Sum;
LastUsed->Count = 2 << ++LastUsed->Shift;
}
}
Changing the sum and count of tests by two times (that means increasing Shift by 1), doesn’t change the current result because it is the same as:
8 >> 3 = 1
16 >> 4 = 1
However, this reduces the speed of adaptation for this see_context. The resulting MEAN will be less sensitive to changes in Sum. For example, let’s assume Sum is equal to 2024, and imagine that we encoded the ESC, and by doing this we increased Sym by 400:
2024 >> 4 = 126
2424 >> 4 = 151
But if the Sym were equal to 4048:
4048 >> 5 = 126
4448 >> 5 = 139
Update
When adding new symbols in the update() function, the initial frequency of the symbol in the context will now be assigned adaptively based on the weighting of certain values. For you, as well as for me, if you have recently become interested in compression, it may not be clear why certain coefficients are calculated in a particular way and not in another. However, we can still at least look at how it can be done for ourselves. It’s entirely possible that there is no precise answer here, and the parameters and the method of their weighting reflect the author’s statistical research. All of this changes between PPMd versions.
Beginning update() by defining the starting coefficients and updating SEE->LastUsed.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void update()
{
context_data** StackPtr = ContextStack;
context* ContextAt = MaxContext;
u32 f0 = LastEncSym->Freq;
u32 cf = LastEncSym->Freq - 1;
u32 sf = MinContext->TotalFreq - MinContext->SymbolCount;
u32 s0 = sf - cf;
u8 InitFreq;
SEE->updateLastUsed();
...// add symbol to contexts, allocate new context
}
Currently, the coefficients cf and sf will be the same for all contexts that don’t have symbols. Later, for non-empty contexts, they will be calculated separately for each of them.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void update()
{
...// init start coeficient
if (ContextAt->SymbolCount == 0)
{
if (MinContext->SymbolCount == 1)
{
InitFreq = f0;
}
else
{
u32 CalcInitFreq = 1;
u32 MoreC = (cf + s0 - 1) / s0;
u32 LessC = (4 * cf > s0) ? 1 : 0;
CalcInitFreq += (cf <= s0) ? LessC : MoreC;
InitFreq = SafeTruncateU32(CalcInitFreq);
}
do
{
context_data* First = ContextAt->Data;
First->Symbol = LastEncSym->Symbol;
First->Freq = InitFreq;
ContextAt->SymbolCount = 1;
ContextAt = ContextAt->Prev;
*StackPtr++ = First;
} while (ContextAt->SymbolCount == 0);
}
...// add symbol for context, allocate new context
}
If MinContext is a binary context, then the frequency of the new symbol will be equal to the frequency of the recently encoded symbol. Otherwise, we check whether the frequency of the encoded symbol occupies a significant portion of the total symbol frequency in MinContext, and based on this, we choose the initial frequency to assign. In the next step, when adding a symbol to non-empty contexts, we first calculate the TotalFreq increment from exiting the context event.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void update()
{
...// init start coefficient
...// init context with SymbolCount == 0
context_data* NewSym;
for (; ContextAt != MinContext; ContextAt = ContextAt->Prev, *StackPtr++ = NewSym)
{
u16 OldCount = ContextAt->SymbolCount;
NewSym = allocSymbol(ContextAt);
if (!NewSym)
{
ContextAt = nullptr;
break;
}
if (OldCount == 1)
{
context_data* First = ContextAt->Data;
if (First->Freq < ((MAX_FREQ / 4) - 1)) First->Freq += First->Freq;
else First->Freq = MAX_FREQ - 4;
ContextAt->TotalFreq = InitEsc + First->Freq + (MinContext->SymbolCount > 3);
}
else
{
u16 AddFreq = (2 * ContextAt->SymbolCount < MinContext->SymbolCount) ? 1 : 0;
u16 tmp = (4 * ContextAt->SymbolCount <= MinContext->SymbolCount) ? 1 : 0;
tmp &= (ContextAt->TotalFreq <= (8 * ContextAt->SymbolCount)) ? 1 : 0;
AddFreq += tmp * 2;
ContextAt->TotalFreq += AddFreq;
}
...// calculate InitFreq
}
}
Here we are using the value of InitEsc that was assigned during the encoding ESC from a binary context. For non-binary contexts, the increase will be 1 if the count of symbols in ContextAt is two times smaller compared to MinContext, and 3 if the count of symbols is four times smaller and their average frequency is 8. The starting frequency of the symbol for non-binary contexts is also set adaptively.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void update()
{
...// init start coefficient
...// init context with SymbolCount == 0
context_data* NewSym;
for (; ContextAt != MinContext; ContextAt = ContextAt->Prev, *StackPtr++ = NewSym)
{
...// add symbol
cf = 2 * f0 * (ContextAt->TotalFreq + 6);
sf = s0 + ContextAt->TotalFreq;
if (cf < 6 * sf)
{
InitFreq = 1 + (cf >= sf) + (cf >= 4 * sf);
ContextAt->TotalFreq += 3;
}
else
{
InitFreq = 4 + (cf >= 9 * sf) + (cf >= 12 * sf) + (cf >= 15 * sf);
ContextAt->TotalFreq += InitFreq;
}
NewSym->Freq = InitFreq;
NewSym->Symbol = LastEncSym->Symbol;
}
}
I don’t know why cf and sf are set in that way, but it seems that the idea is to correlate the frequency of the encoded symbol with the overall frequency of higher-order contexts, taking into account its portions in the MinContext total sum. This way, for example, some younger contexts will receive a higher initial value for the new symbol.
Rescale
If we try to run the test, it will not work since we are doing rescale() wrong. We need to account that the value of ESC is now held in TotalFreq. Let’s make a minimal fix and see what happens.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void rescale(context* Context)
{
u32 EscFreq = Context->TotalFreq;
Context->TotalFreq = 0;
for (u32 i = 0; i < Context->SymbolCount; ++i)
{
context_data* Symbol = Context->Data + i;
EscFreq -= Symbol->Freq;
u32 NewFreq = (Symbol->Freq + 1) / 2;
Symbol->Freq = NewFreq;
Context->TotalFreq += NewFreq;
}
Context->TotalFreq += EscFreq;
}
| name | H | file size | compr. size | bpb | Sym | ESC |
|---|---|---|---|---|---|---|
| book1 | 4.572 | 768771 | 218066 | 2.269 | 192541.4 | 25500.5 |
| geo | 5.646 | 102400 | 57082 | 4.4595 | 51463.4 | 5610.4 |
| obj2 | 6.26 | 246814 | 74016 | 2.399 | 63014 | 10982.5 |
| pic | 1.21 | 513216 | 113368 | 1.767 | 107108.9 | 6252.6 |
| Intel.pdf | 7.955 | 26192768 | 24035022 | 7.34 | 22460985.9 | 1570794.9 |
We get better results for all files except pic, which again become bigger. The problem lies in the Order-N contexts that we don’t free from symbols that have not appeared there for a long time, due to which the coding efficiency drops greatly for this kind of data. Interesting that the first method of context tree building when we did a full search for the current context starting from the very beginning, didn’t have such a problem, and basic PPMC compressed pic to 0.818 bpb. We will fix it now and, in addition, add symbol sorting at rescale(). I also took the implementation of this from ppmdf. The code within the function body will get a little bigger, but it consists only of basic operations.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void rescale(context* Context)
{
context_data Temp;
LastEncSym->Freq += 4;
Context->TotalFreq += 4;
context_data* First = Context->Data;
u32 MoveCount = LastEncSym - Context->Data;
if (MoveCount)
{
Temp = *LastEncSym;
for (u32 i = MoveCount; i > 0; i--)
{
Context->Data[i] = Context->Data[i - 1];
}
*First = Temp;
LastEncSym = First;
}
u32 MaxCtxAdder = (Context != MaxContext) ? 1 : 0;
u32 EscFreq = Context->TotalFreq - First->Freq;
First->Freq = (First->Freq + MaxCtxAdder) >> 1;
Context->TotalFreq = First->Freq;
...
}
Starting with that, we add a bonus to the symbol that called rescale() and move it to the first position in the context’s symbol array if it’s not already there. MaxCtxAdder is the value that will prevent the symbol frequency from becoming less than 1 if it’s not in the CM(N) context.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void rescale(context* Context)
{
...// move caller symbol to position 0
for (u32 SymbolIndex = 1; SymbolIndex < Context->SymbolCount; SymbolIndex++)
{
context_data* Symbol = Context->Data + SymbolIndex;
EscFreq -= Symbol->Freq;
Symbol->Freq = (Symbol->Freq + MaxCtxAdder) >> 1;
Context->TotalFreq += Symbol->Freq;
context_data* Prev = Symbol - 1;
if (Symbol->Freq > Prev->Freq)
{
for (;;)
{
context_data* NextPrev = Prev - 1;
if ((NextPrev != First) && (Symbol->Freq > NextPrev->Freq)) Prev = NextPrev;
else break;
}
u32 MoveCount = Symbol - Prev;
if (MoveCount)
{
Temp = *Symbol;
for (u32 i = SymbolIndex; MoveCount > 0; i--, MoveCount--)
{
Context->Data[i] = Context->Data[i - 1];
}
*Prev = Temp;
}
}
}
...
}
Then we continue to divide the symbol frequency by 2, checking if it is in sorted order. If necessary, we move it up, but now relative to its position, since MoveCount now is the difference between symbols. Finally, at the end, we decrease the SymbolCount by the number of symbols with a frequency of 0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void rescale(context* Context)
{
...// rescale and sort symbol
context_data* LastSym = Context->Data + (Context->SymbolCount - 1);
if (LastSym->Freq == 0)
{
u32 ToRemove = 0;
do
{
++ToRemove;
--LastSym;
} while (LastSym->Freq == 0);
EscFreq += ToRemove;
Context->SymbolCount -= ToRemove;
if (Context->SymbolCount == 1)
{
do
{
First->Freq -= (First->Freq >> 1);
EscFreq >>= 1;
} while (EscFreq > 1);
SubAlloc.shrink(Context->Data, 1);
return;
}
}
EscFreq -= EscFreq >> 1;
Context->TotalFreq += EscFreq;
}
In the case where only one symbol remains, there seems to be some sense in normalizing its frequency. I cannot say for certain. If we don’t change its frequency along with ESC, then the result for tested files will not be affected much. The most benefit from this was obtained by pic, which decreased by 58 bytes.
Result
| name | H | file size | compr. size | bpb | Sym | ESC |
|---|---|---|---|---|---|---|
| book1 | 4.572 | 768771 | 216815 | 2.256 | 187983.2 | 28806.5 |
| geo | 5.646 | 102400 | 56712 | 4.43 | 50937.9 | 5766.4 |
| obj2 | 6.26 | 246814 | 73397 | 2.379 | 61953.8 | 11423 |
| pic | 1.21 | 513216 | 50456 | 0.787 | 37795.3 | 12616.8 |
| Intel.pdf | 7.955 | 26192768 | 24033789 | 7.34 | 22459090.5 | 1571454.9 |
Much nicer! As seen, the main part of compression was made in the previous part, so to speak. In general, you can always improve compression results by doing more work by combining various techniques, etc. Perhaps this is one of the main reasons why LZ methods have gained such popularity for general purpose compression as their encoder and decoder can be asymmetrical, unlike PPM, a good part of the modeling work can be offloaded to the encoding part since fast decoding for such things is what we would like to have. Just out of curiosity, we can check how far our simple model is from, for example, LZMA. For this purpose, I ran 7z with parameters -m0=LZMA2 -mx=9 -md=10m and took time from user colon.
| name | compr. size | bpb | enc time | dec time |
|---|---|---|---|---|
| book1 | 261157 | 2.718 | 0.133 | 0.008 |
| geo | 53305 | 4.154 | 0.01 | 0.005 |
| obj2 | 61547 | 1.995 | 0.025 | 0.005 |
| pic | 41991 | 0.655 | 0.035 | 0.003 |
| Intel.pdf | 22644438 | 6.916 | 2.4 | 0.84 |
It’s not a surprise that such an advanced LZ coder outperformed our simple 1k lines PPM model in all aspects, but since book1 fits very well into PPM’s data type, it compressed it better by 0.48 bpb than LZMA.
Source code for this part.
References
[1] PPMZ https://www.cbloom.com/src/ppmz.html
[2] Secondary Estimation : From PPMZ SEE to PAQ APM https://cbloomrants.blogspot.com/2018/05/secondary-estimation-from-ppmz-see-to.html
[3] PPM: one step to practicality http://ctxmodel.net/files/PPMd/ShkarinPPMII.pdf
[4] J version by Eugene D. Shelwien https://github.com/Shelwien/ppmd_sh